学而思奥数天天练栏目每日精选中等、高等难度试题各一道。中难度试题适合一些有过思维基础训练、考题学习经历,并且奥数成绩中上的学生。高难度试题立足于杯赛真题、综合应用和加深各知识点,适合一些志在竞赛 中夺取佳绩的学生。
·本周试题由学而思奥数名师徐研精选、解析,以保证试题质量。
·每周末,我们将一周试题汇总为word版本试卷,您可下载打印或在线阅读。
·每道题的答题时间不应超过15分钟。
难度:★★★★
小学四年级奥数天天练:计算
求2+7+12+17+…+192+197的值。
解答:这是一列公差为5的等差数列的求和问题。我们看到首末两项的和以及与首末等距离的两项的和都是199。求这个数列的和,我们只要用首末两项的和乘以项数再除以2就可以了。这样我们得到了等差数列的求和公式:
数列和=首末项的和×项数÷2
其中项数=首末两项差÷公差+1
解 3+7+12+17+…+192+197
=(2+197)×[(197-2)÷5+1]÷2
=3980
难度:★★★★★
小学四年级奥数天天练:计算
在各个方格中填上适当的数字。

解答:从乘数的个位上数字6考虑,6与被乘数的乘积在个位上是4,则被乘数的个位上只能是4或9。第二行乘积的末尾是0,所以9是不可能的。由于6×4=24,进位2,乘积的十位是0,知被乘数的十位是8或3。由于与6的乘积是四位数,那么被乘数的千位只能是1。知被乘数是1284或1234。
被乘数与乘数的十位上数字的乘积在个位上是0,知乘数的十位上是5。再从乘积的十位是7,就可确定被乘数的十位是3。所以,原式应是
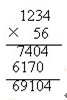
对于填数字问题,解答时一定要充分利用已知数字,分析式子中隐含的数字间的关系,逐个突破。





