学而思奥数天天练栏目每日精选中等、高等难度试题各一道。中难度试题适合一些有过思维基础训练、考题学习经历,并且奥数成绩中上的学生。高难度试题立足于杯赛真题、综合应用和加深各知识点,适合一些志在竞赛 中夺取佳绩的学生。
·本周试题由学而思奥数名师刘森精选、解析,以保证试题质量。
·每周末,我们将一周试题汇总为word版本试卷,您可下载打印或在线阅读。
·每道题的答题时间不应超过15分钟。
难度:★★★★
小学四年级奥数天天练:几何计数
如图,用9枚钉子钉成水平和竖直间隔都为1厘米正方阵.用一根橡皮筋将3枚不共线的钉子连接起来就形成一个三角形.在这样得到的三角形中,面积等于1平方厘米的三角形共有多少个?

【分析】要充分利用图形的对等性.这个三角形可以底为1,高为2;也可以底为2,高为1.
(1)等腰直角三角形(如图1):底为2,高为1,共8个;
(2)直角三角形(如图2):16个;
(3)钝角三角形(如图3):8个
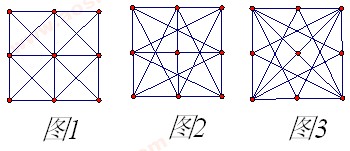
综上,面积为1的三角形共32个.
评注:这种利用对称性,寻找基本图形的思路,在杯赛中经常考到.
难度:★★★★★
小学四年级奥数天天练:计数问题
如果一个大于9的整数,其每个数位上的数字都比它右边数位上的数字小,那么我们称它为"迎春数".那么,小于2008的"迎春数"共有 个。
【分析】这是一道组合计数问题.
方法一:枚举法――按位数分类计算.
一、两位数中,"迎春数"个数
(1)十位数字是1,这样的"迎春数"有12,13,…,19,共8个;
(2)十位数字是2,这样的"迎春数"有23,…,29,共7个;
(3)十位数字是3,这样的"迎春数"有34,…,39,共6个;
(4)十位数字是4,这样的"迎春数"有45,…,49,共5个;
(5)十位数字是5,这样的"迎春数"有56,…,59,共4个;
(6)十位数字是6,这样的"迎春数"有67,68,69,共3个;
(7)十位数字是7,这样的"迎春数"有78,79,共2个;
(8)十位数字是8,这样的"迎春数"只有89这1个;
(9)没有十位数字是9的两位的"迎春数";
所以两位数中,"迎春数"共有36个.
二、三位数中,"迎春数"个数
(1)百位数字是1,这样的"迎春数"有123-129,134-139,…,189,共28个;
(2)百位数字是2,这样的"迎春数"有234-239,…,289,共21个;
(3)百位数字是3,这样的"迎春数"有345-349,…,389,共15个;
(4)百位数字是4,这样的"迎春数"有456-459,…,489,共10个;
(5)百位数字是5,这样的"迎春数"有567-569,…,589,共6个;
(6)百位数字是6,这样的"迎春数"有678,679,689,共3个;
(7)百位数字是7,这样的"迎春数"只有789,这1个;
(8)没有百位数字是8,9的三位的"迎春数";
所以三位数中,"迎春数"共有84个.
三、1000-1999的自然数中,"迎春数"个数
(1)前两位数字是12,这样的"迎春数"有1234-1239,…,1289,共21个
(2)前两位数字是13,这样的"迎春数"有1345-1349,…,1389,共15个;
(3)前两位数字是14,这样的"迎春数"有1456-1459,…,1489,共10个;
(4)前两位数字是15,这样的"迎春数"有1567-1569,…,1589,共6个;
(5)前两位数字是16,这样的"迎春数"有1678,1679,1689,共3个;
(6)前两位数字是17,这样的"迎春数"只有1789这1个;
(7)没有前两位数字是18,19的四位的"迎春数";
所以四位数中,"迎春数"共有56个.
四、2000-2008的自然数中,没有"迎春数"
所以小于2008的自然数中,"迎春数"共有36+84+56=176 个.
方法二:利用组合原理?
小于2008的"迎春数",只可能是两位数、三位数和1000多的数.
计算两位 "迎春数"的个数,它就等于从1-9这9个数字中任意取出2个不同的数字,
每一种取法对应于一个"迎春数",即有多少种取法就有多少个"迎春数".显然不同的取
法有9×8÷2=36 中,所以两位的"迎春数"共有36个.
同样计算三位数和1000多的数中"迎春数"的个数,它们分别有 9×8×7÷3÷2÷1=84个和8×7×6÷3÷2÷1=56 个.
所以小于2008的自然数中,"迎春数"共有36+84+56=176 个。






