学而思奥数天天练栏目每日精选一套高等难度的试题,各年级分开,配有详细答案及试题解析,此类试题立足于杯赛真题、综合应用和加深各知识点,适合一些志在竞赛中夺取佳绩的学生。
·本试题由武汉学而思奥数全职教师魏俐光老师精选、解析,以保证试题质量

名师介绍: 北京大学双学位毕业,学而思竞赛团队武汉负责人,华杯赛阅卷组成员,华杯赛、希望杯浙江赛区一等奖、全国初中数学联赛一等奖、全国高中数学联赛二等奖,浙江省余姚市高考理科状元,多年奥数教学经历,带领邵子涵、刘文轩等20多名学员获得华杯赛、迎春杯等一等奖。教学特色: 教学过程中注重和孩子的沟通和交流,力求用最简单朴实的语言教给孩子奥数的知识;课堂气氛活跃,风趣幽默;注重对孩子数学兴趣的培养、解题技巧的提高、好的学习习惯的积累。
·每道题的答题时间不应超过15分钟
·您可以按“下载适合打印版本试卷”获得word版本试卷进行打印。
一年级答案:
每隔3页放进一片树叶,15页共有如图所示,
□□□○□□□○□□□○□□□○□□□
需要放进4片叶子
二年级答案:
解:①5÷5+(5-5)×5=1
(5+5)÷5-(5÷5)=1
②(5+5)÷5+5-5=2
5-(5+5+5)÷5=2
③5÷5+(5+5)÷5=3
5-5÷5-5÷5=3
④(5+5+5+5)÷5=4
5-5÷5+5-5=4.
三年级答案:
要是这个算是尽可能大,将每个空用字母表示:
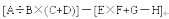
因此必须使A、C、D、H尽可能大,B、E、F、G尽可能小,于是:
A=9,C=8,D=7,H=6,B=1,E=2,F=3,G=4,则此时为:
[9÷1×(8+7)]-[2×3+4-6]=131
四年级答案:
(a,b,c)=15=3×5,所以a,b,c中都含有1个3,1个5。(a,b)=75=3×5×5,所以a,b中都含有1个3,2个5。
[a,b]=450=2×3×3×5×5,因为a>b,a可能再含有1个3,b再含有1个2;或者a含有1个6,b含有1个1。
[b,c]=1050=2×3×5×5×7,因为b>c,所以b中还含有1个2,c中还含有1个7
即:b=3×5×5×2=150,c=3×5×7=105,a=3×5×5×3=225
答:c是105。
五年级答案:
答对三道题或三道题以上的人算及格,要使100人中,及格人数尽可能少则需使每人首先都答对其中的两题,余下(81+91+85+79+74)-2×100=410-200=210道尽量分配给少数人,这少数人中每人最多再对3道所以210÷(5-2)=70(人)即在这100人中,至少有70人及格。
六年级答案:
这道题并不是品种单一,不能够容易地找到抽屉和苹果,由于有三种颜
色的筷子,而且又混杂在一起,为了确保取出的筷子中有2双不同颜色的筷子,可以分两步进行。第一步先确保取出的筷子中有1双同色的;第二步再从余下的筷子中取出若干根保证第二双筷子同色。 首先,要确保取出的筷子中至少有1双是同色的,我们把黑色、白色、黄色三种颜色看作3个抽屉,把筷子当作苹果,根据抽屉原则,只需取出4根筷子即可。其次,再考虑从余下的20根筷子中取多少根筷子才能确保又有1双同色筷子,我们从最不利的情况出发,假设第一次取出的4根筷子中,有2根黑色,1根白色,1根黄色。这样,余下的20根筷子,有6根黑色的,7根白色的,7根黄色的,因此,只要再取出7根筷子,必有1根是白色或黄色的,能与第一次取出的1根白色筷子或黄色筷子配对,从而保证有2双筷子颜色不同,总之,在最不利的情况下,只要取出4+7=11根筷子,就能保证达到目的。




